Playing With History
Part 1: Overview
In this project, we focused on probability as well as types of probability by working on different worksheets and really diving into whatever current topic we were focused on to fully understand it step by step. The first assignment was the Game of Pig where we rolled dice and if a certain number was rolled, one outcome was produced, and if other numbers were rolled another outcome was produced. We did other games like this throughout the project as we learned different subtopics in probability. We were expected to learn the following, I also added descriptions so that you can well understand what I’m referring to.
In this project, we focused on probability as well as types of probability by working on different worksheets and really diving into whatever current topic we were focused on to fully understand it step by step. The first assignment was the Game of Pig where we rolled dice and if a certain number was rolled, one outcome was produced, and if other numbers were rolled another outcome was produced. We did other games like this throughout the project as we learned different subtopics in probability. We were expected to learn the following, I also added descriptions so that you can well understand what I’m referring to.
- Probability (definition)
- def: the likelihood of something happening; the extent to which an event is likely to occur, measured by the ratio of the favorable cases to the whole number of cases possible
- Observed Probability
- The probability or results which occur and are observed when testing for probability of outcomes. (Who’s Cheating: Observed Results Worksheet)
- Theoretical Probability
- The predicted probability of what would occur, written as the number of favorable outcomes / the number of possible outcomes. (Two-Dice Sums: Theoretical Probabilities)
- Conditional Probability
- The probability of an event given that another event has occurred to cause the other. (Who’s Cheating: Predicted Results Worksheet)
- Probability of Multiple Events
- The probability after two or more events happening. You would multiply Probability 1 by Probability 2 and so on depending on how many events there are to find the probability. (Colorblind)
- Expected Value
- The predicted value of an occurrence happening. You would multiply the population - number of trials or events - by the current probability you would be considering - the calculated likeliness of its occurrence - to find the expected value. (The Breast Cancer Problem)
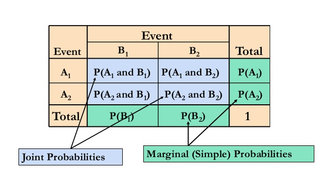
- Two-Way Tables
- A table giving sections for both joint and marginal probabilities - scroll down for explanation of probabilities - to better organize data and find different probabilities. (Dr. Drew, The Dog Ate My Homework!)
- Tree Diagram
- A “family tree” style diagram to connect multiple events and give a path to find one or more probabilities. Click here to see set-up of Tree Diagram. (Probability Tree Practice)
- Joint Probability
- A statistical measure where the likelihood occurring together and at the same time is calculated, the probability of Event A happening at the same time as Event B. ONe example would be a woman/man (Event A/A’) reading/not reading (Event B/B’). We would look for probability A and B, also written as Pr [A and B]. We would calculate the probability by multiplying A by B.
- Marginal Probability
- After collecting variables which could go in a Two-Way Table - scroll up for explanation of table - the marginal probabilities are the totals which combine the Event A and B in its row or column. It gives the probabilities of various values of the variables without reference to the value of other variables.
Part 2: Renaissance-Inspired Game
The Renaissance game my partner and I chose is called Knucklebones. Although the specific details of its origin are unknown, it’s widely believed it originated in Ancient Greece when Sophocles ascribed the invention of knucklebones to the mythical figure Palamedes, who then taught it to his Greek countrymen during the Trojan War. This game can actually be played in multiple ways. The first, more primitive method is to toss up and then catch the bones on the back of the hand, much like today’s modern game of Jacks. This form of the game was usually played by women and children, and could also be called five-stones. There were varieties of this form of the game such as one where the bones were thrown into holes in the earth. The second, more derivative way is pure chance, stones thrown upon a table out of a hand or cup and then values counted by what side faced down on the table instead of facing up, similar to today’s dice games were rolling a dice determines point value, movement on a board, or probability. Since we decided to modernize our game for this project, we used six-sided dice instead of stones. We also made a pamphlet which explains our game, all of the rules and requirements, and how to keep score and play fair. There isn’t much to it since it is so much based on dice rolling and pure chance. Click here to view the pamphlet for more information on our game. My partner and I chose this game to exhibit because it interested us since it could be played multiple ways and seemed like a good game to connect probability to. The probability and chance in the game is pretty obvious and actually the core of the game’s structure. The chance in what number is rolled with the two dice, the probability of rolling specific sums, and the probability of how many rolls it will take to reach a specific score are all attributes to what role probability takes in our game.
The Renaissance game my partner and I chose is called Knucklebones. Although the specific details of its origin are unknown, it’s widely believed it originated in Ancient Greece when Sophocles ascribed the invention of knucklebones to the mythical figure Palamedes, who then taught it to his Greek countrymen during the Trojan War. This game can actually be played in multiple ways. The first, more primitive method is to toss up and then catch the bones on the back of the hand, much like today’s modern game of Jacks. This form of the game was usually played by women and children, and could also be called five-stones. There were varieties of this form of the game such as one where the bones were thrown into holes in the earth. The second, more derivative way is pure chance, stones thrown upon a table out of a hand or cup and then values counted by what side faced down on the table instead of facing up, similar to today’s dice games were rolling a dice determines point value, movement on a board, or probability. Since we decided to modernize our game for this project, we used six-sided dice instead of stones. We also made a pamphlet which explains our game, all of the rules and requirements, and how to keep score and play fair. There isn’t much to it since it is so much based on dice rolling and pure chance. Click here to view the pamphlet for more information on our game. My partner and I chose this game to exhibit because it interested us since it could be played multiple ways and seemed like a good game to connect probability to. The probability and chance in the game is pretty obvious and actually the core of the game’s structure. The chance in what number is rolled with the two dice, the probability of rolling specific sums, and the probability of how many rolls it will take to reach a specific score are all attributes to what role probability takes in our game.
|
Part 3: Probability Analysis
Question #1:
Habits of a Mathematician:
|
|
Question #2:
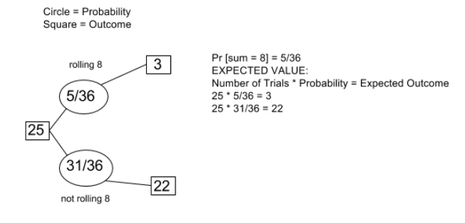
- If you rolled two dice 5 times, what’s the probability the sum of the dice equals 8 at least once? Probability Tree/Calculations: First to find the answer to this question, we need to understand the probability of a sum of 8 being rolled or not rolled. We made our probability tree to show what the chances were for each option. After finding the probabilities, we used the equation given to solve what the probability is of rolling a sum of 8 at least once. Habits of a Mathematician:
|
|
Question #3:
- If you rolled two dice three times, what’s the probability the sum of the dice equals 8 all three times? Habits of a Mathematician:
|
Part 4: Reflection
For our project, we created products such as a Renaissance based game and its probability analysis and filled out worksheets so we could understand probability. I was able to go in depth for all of our worksheets and take notes as well to fully comprehend the subject at hand. I did however also have some challenges when it came to the game, or the process of understanding each topic of probability.
Some challenges I faced were when we were creating the math game, since we decided to make our own dice instead of just buying or borrowing some. It took a bit longer than expected, and it was hard to find the right wood to use and the best way to cut it. My partner and I also for a bit of time thought it would be a good idea to make a wooden open box design to roll the dice into so they wouldn’t go flying, but once we completed the open box, it didn’t look as we had hoped. There were uneven sides, it was messy, and unevenly painted, if painted at all. We ended up scrapping the idea, but I’m happy we went for trying because we were still able to test and experiment on what would and wouldn’t work, and got to problem solve even if it didn’t work out in the end. I also was challenged when learning about different topics in probability, such as joint and marginal probability. It took a bit longer for it to click in my head, and at some points I didn’t think I would ever get it. It took a lot of working with my peers and a lot of questions asked and follow-up questions as well, but in the end I was able to answer those questions myself and complete problems that I at first wouldn’t have been able to work out.
I also had success, both in my challenges and in other parts of the project. In my challenges, I was able to use the skills I had acquired - such as creativity, problem solving, and determination - from past projects to complete and understand what I didn’t think I could before. I also had success in many topics of probability, catching on quickly and being able to comprehend and explain the how pretty easily. I was also a pretty good group member when working on the game and probability analysis, and didn’t slack and made sure to do my fair amount of work, inputting my ideas while collaborating and working together to come up with a final product.
This project was overall very positive and let me grow as a student, both through skills and knowledge. I feel that there were definitely challenges along the way, but it all ended up working out. I improved on skills such as determination, creativity, and time management. I also learned a lot about probability, as you can see above. I hope to grow by acquiring new skills and knowledge, and being able to dive deeper in the work I am doing by taking more challenge options and asking for more work or a more advanced option if I can work at that level.