Measuring Your World
Part 1: Overview
In this project, we are focusing on trigonometry and all of the trigonometric formulas to solve different problems. We have been learning how to both understand and proof these different formulas, and how to apply them to various dilemmas. Read below to understand the eight trigonometric formulas taught in class.
1. Sine: trigonometric function that equals the ratio of the side opposite to a given angle to the hypotenuse (right triangle)
2. Cosine: trigonometric function that equals the ratio of the side adjacent to an acute angle to the hypotenuse (right triangle)
3. Tangent: trigonometric function that equals the ratio of the side opposite to a given angle to the adjacent to the angle and hypotenuse (right triangle)
4. ArcSine: inverse of sine function
5. ArcCosine: inverse of cosine function
6. ArcTangent: inverse of tangent function
7. Law of Sines: equation which connects the lengths of the sides of a triangle to the sines of its angles
8. Law of Cosines: equation which connects the lengths of the sides of a triangle to the cosines of its angles
Part 2: Narrative
The first part of our project was learning and proving the Pythagorean Theorem. The formula is a^2 + b^2 = c^2, and represents the sides of the triangle; a and b = adjacent and opposite and c = hypotenuse. This equation can be used to find a missing side length of any right triangle. We were able to test out the theorem when measuring right triangles and splitting them. We were able to prove the formula works by finding the distance formula out of the theorem. We found this formula by using a Cartesian coordinate plane. We were then able to use the different radius lines as a hypotenuse, and used the x and y axis as "measurements". All the points are equidistant from the center point of the circle, which means each point has the same radius length.
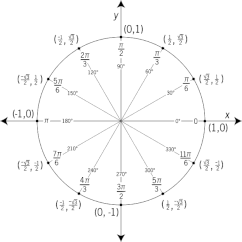
The next part of our project was understanding and using the Unit Circle. It's a tool we were able to use to find the coordinate point on the circle of a specific right triangle. We would need to reflect the right triangle we were solving for sometimes to better solve for the length. We also used sine to find the y coordinate, and since the cosine function is opposite of sine, we inversed the function for cosine. We used the angle of the y axis to find the x coordinate. We then found the tangent function by reflecting the hypotenuse over the x axis, showing a perfect 90 degree angle.
We then learned how to find the coordinate point of a right triangle with the angle closest to the center of 30 degrees, 45 degrees, and 60 degrees. To find 30 degrees, we took that right triangle and reflected it over the x axis. That then created an equilateral triangle, as we know that an equilateral triangle would have all three angles 60 degrees, and that's what the combines triangle would account to. We then know that all side lengths need to be the same for that equilateral triangle, and since we know the radius (one side), we can figure out the other two sides and use common knowledge and division to find all three lengths of the original right triangle. For 45 degrees, we realized it was an isosceles triangle. That lets you know that two of the three sides will be equivalent and therefore x will equal y. Once we know one side, we can find the other by using x = y, and the third with our trigonometric functions. For 60 degrees, we found that it was simply opposite of 30 degrees, and instead of that right triangle being reflected on the x axis, it would have been reflected on the y axis. Because it is "flipped" in this sense, we can also state that the coordinates would be flipped from the 30 degrees ones. You just switch what x and y were for 30 degrees so that x becomes y and y becomes x.
To understand the Law of SInes, we were given the Mount Everest problem, where we had an isosceles triangle with one known length and no right angles, but the given angles labeled. The challenge was to find the missing lengths, and to do so we had to take the triangle apart into smaller triangles with right angles. We then found the Law of Sines while trying to solve. Since we only knew one side, we had to use an equation which could use the angles primarily to solve. Law of SInes is also known as ASA (angle, side, angle) so you only need to know one side and two connecting angles to solve for other lengths.
In this project, we are focusing on trigonometry and all of the trigonometric formulas to solve different problems. We have been learning how to both understand and proof these different formulas, and how to apply them to various dilemmas. Read below to understand the eight trigonometric formulas taught in class.
1. Sine: trigonometric function that equals the ratio of the side opposite to a given angle to the hypotenuse (right triangle)
2. Cosine: trigonometric function that equals the ratio of the side adjacent to an acute angle to the hypotenuse (right triangle)
3. Tangent: trigonometric function that equals the ratio of the side opposite to a given angle to the adjacent to the angle and hypotenuse (right triangle)
4. ArcSine: inverse of sine function
5. ArcCosine: inverse of cosine function
6. ArcTangent: inverse of tangent function
7. Law of Sines: equation which connects the lengths of the sides of a triangle to the sines of its angles
8. Law of Cosines: equation which connects the lengths of the sides of a triangle to the cosines of its angles
Part 2: Narrative
The first part of our project was learning and proving the Pythagorean Theorem. The formula is a^2 + b^2 = c^2, and represents the sides of the triangle; a and b = adjacent and opposite and c = hypotenuse. This equation can be used to find a missing side length of any right triangle. We were able to test out the theorem when measuring right triangles and splitting them. We were able to prove the formula works by finding the distance formula out of the theorem. We found this formula by using a Cartesian coordinate plane. We were then able to use the different radius lines as a hypotenuse, and used the x and y axis as "measurements". All the points are equidistant from the center point of the circle, which means each point has the same radius length.
The next part of our project was understanding and using the Unit Circle. It's a tool we were able to use to find the coordinate point on the circle of a specific right triangle. We would need to reflect the right triangle we were solving for sometimes to better solve for the length. We also used sine to find the y coordinate, and since the cosine function is opposite of sine, we inversed the function for cosine. We used the angle of the y axis to find the x coordinate. We then found the tangent function by reflecting the hypotenuse over the x axis, showing a perfect 90 degree angle.
We then learned how to find the coordinate point of a right triangle with the angle closest to the center of 30 degrees, 45 degrees, and 60 degrees. To find 30 degrees, we took that right triangle and reflected it over the x axis. That then created an equilateral triangle, as we know that an equilateral triangle would have all three angles 60 degrees, and that's what the combines triangle would account to. We then know that all side lengths need to be the same for that equilateral triangle, and since we know the radius (one side), we can figure out the other two sides and use common knowledge and division to find all three lengths of the original right triangle. For 45 degrees, we realized it was an isosceles triangle. That lets you know that two of the three sides will be equivalent and therefore x will equal y. Once we know one side, we can find the other by using x = y, and the third with our trigonometric functions. For 60 degrees, we found that it was simply opposite of 30 degrees, and instead of that right triangle being reflected on the x axis, it would have been reflected on the y axis. Because it is "flipped" in this sense, we can also state that the coordinates would be flipped from the 30 degrees ones. You just switch what x and y were for 30 degrees so that x becomes y and y becomes x.
To understand the Law of SInes, we were given the Mount Everest problem, where we had an isosceles triangle with one known length and no right angles, but the given angles labeled. The challenge was to find the missing lengths, and to do so we had to take the triangle apart into smaller triangles with right angles. We then found the Law of Sines while trying to solve. Since we only knew one side, we had to use an equation which could use the angles primarily to solve. Law of SInes is also known as ASA (angle, side, angle) so you only need to know one side and two connecting angles to solve for other lengths.
Part 3: Project Process
For our actual product, we measured a #2 Dixon Ticonderoga pencil because it is a very popular object with multiple geometric shapes - a hexagonal cylinder, cone, and cylinder. For this item, we split the pencil into these shapes and were able to find what we needed out of each shape and then combine our answers to get the total answer.
We had to complete multiple mathematical functions; a trigonometric function, area formula, and volume formula. We had to use prior knowledge and common sense to find the solutions. For the trigonometric function, we decided to show a proof of the regular hexagon leading to an equilateral triangle. Because it is a regular hexagon, and the exterior angles must equal 360 degrees. 360 divided by 6 is 60 degrees, which must be the inside angle. Since it's regular, all angles and sides will be the same. Since it's a hexagon, it's also symmetrical if you split it down the middle from one point to it's directly opposing one. We can then conclude that by drawing a line through the opposing points, we will be able to create six equilateral triangles within the hexagon. Since all interior angles are 60 degrees, we know that the third must be 60 degrees as well. This conclusion leads us into the area formula, where by using the equilateral triangles and turning them into perfect right triangles. I knew the measurements of the pencil and could then plug in what I knew into the formula. Once I found the area, I found the volume of the cone and cylinder and added all of the volumes together to find the total volume of the pencil.
Overall, we had a lot of successes and challenges in this project. some successes I had were collaborating well with my partner and doing all of the math equations right. Some challenges were knowing where our pencil was at all times since it's a smaller and more common object, and measuring correctly. At first we measured in inches, but realized that centimeters would be much more correct and accurate. We then thought it would be good to measure in decimals when it came to completing calculations.
For our actual product, we measured a #2 Dixon Ticonderoga pencil because it is a very popular object with multiple geometric shapes - a hexagonal cylinder, cone, and cylinder. For this item, we split the pencil into these shapes and were able to find what we needed out of each shape and then combine our answers to get the total answer.
We had to complete multiple mathematical functions; a trigonometric function, area formula, and volume formula. We had to use prior knowledge and common sense to find the solutions. For the trigonometric function, we decided to show a proof of the regular hexagon leading to an equilateral triangle. Because it is a regular hexagon, and the exterior angles must equal 360 degrees. 360 divided by 6 is 60 degrees, which must be the inside angle. Since it's regular, all angles and sides will be the same. Since it's a hexagon, it's also symmetrical if you split it down the middle from one point to it's directly opposing one. We can then conclude that by drawing a line through the opposing points, we will be able to create six equilateral triangles within the hexagon. Since all interior angles are 60 degrees, we know that the third must be 60 degrees as well. This conclusion leads us into the area formula, where by using the equilateral triangles and turning them into perfect right triangles. I knew the measurements of the pencil and could then plug in what I knew into the formula. Once I found the area, I found the volume of the cone and cylinder and added all of the volumes together to find the total volume of the pencil.
Overall, we had a lot of successes and challenges in this project. some successes I had were collaborating well with my partner and doing all of the math equations right. Some challenges were knowing where our pencil was at all times since it's a smaller and more common object, and measuring correctly. At first we measured in inches, but realized that centimeters would be much more correct and accurate. We then thought it would be good to measure in decimals when it came to completing calculations.